Local Modeling Perspectives on Scale Issues

The concept of ‘spatial scale’, or simply ‘scale’ is implicit in any discussion of global versus local models. The raison d’etre of local models is that a global scale (where here ‘global’ simply refers to all locations within a predefined area of interest) might be the incorrect scale at which to undertake any analysis of spatial processes; the alternative being a local scale (where here ‘local’ refers to individual locations). Here we explore two well-known scale issues in the context of local modeling: the modifiable areal unit problem (MAUP) and Simpson’s paradox. In doing so, we highlight that scale effects play two very different roles in any consideration of local versus global modeling.

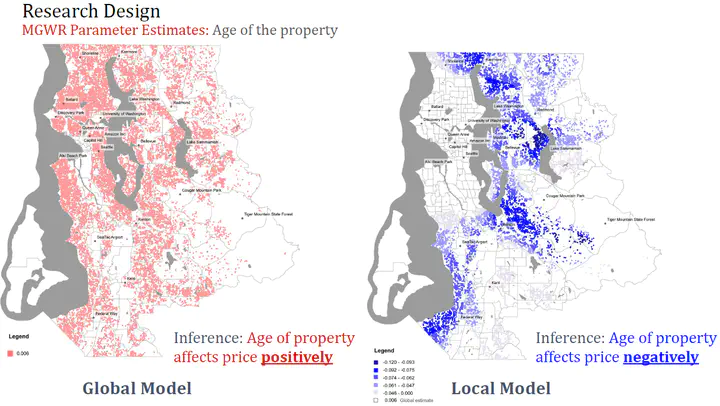
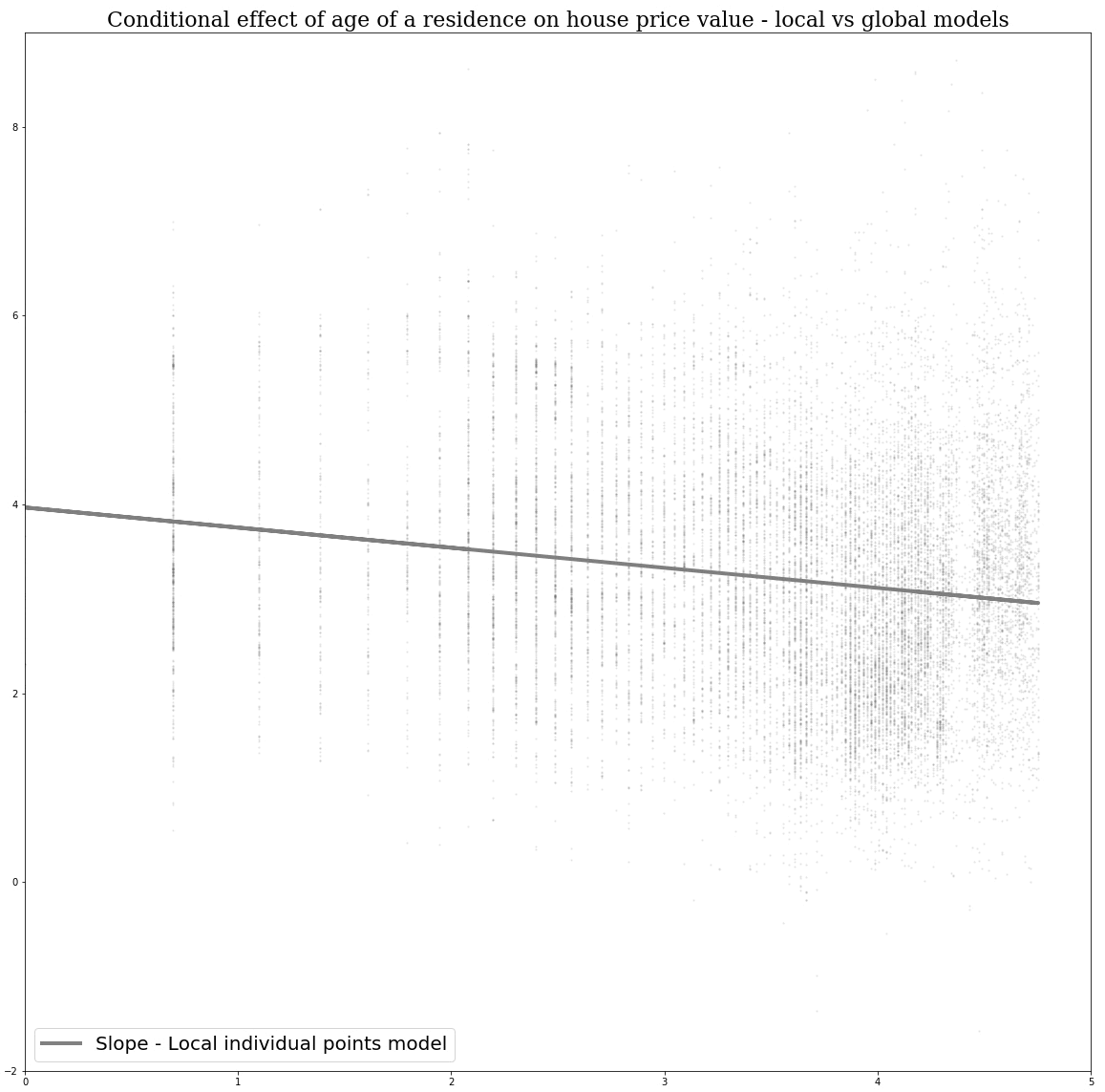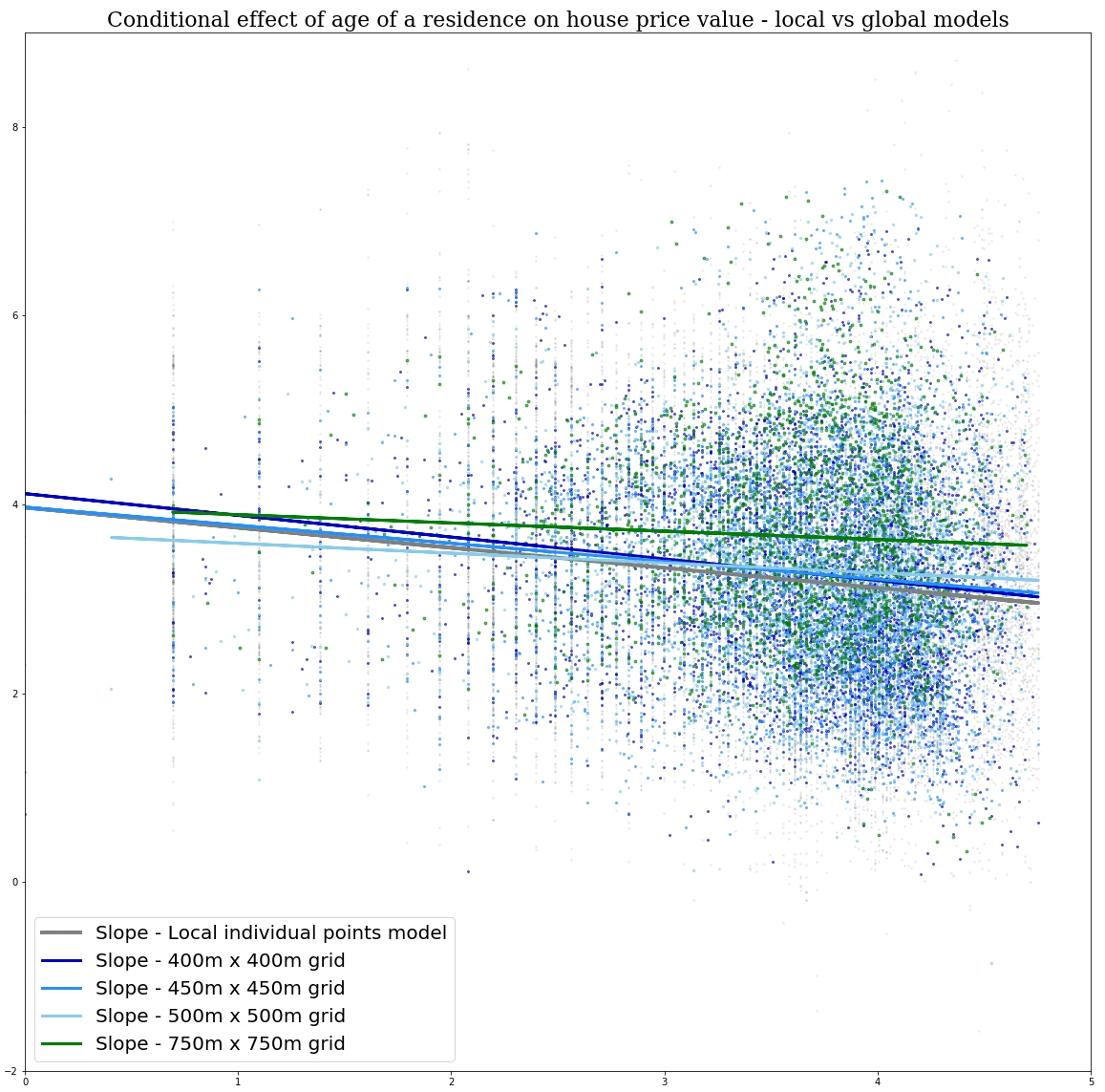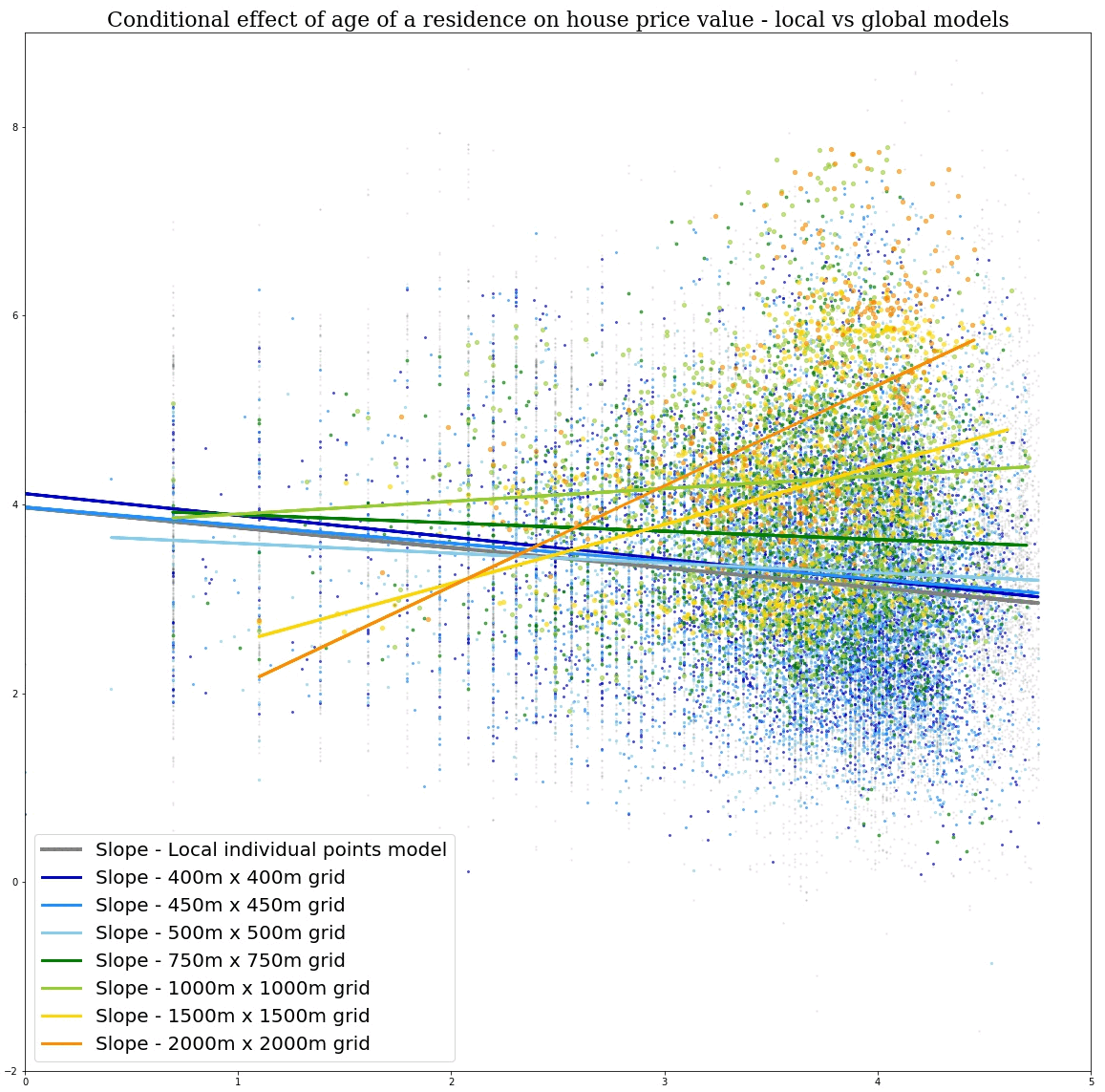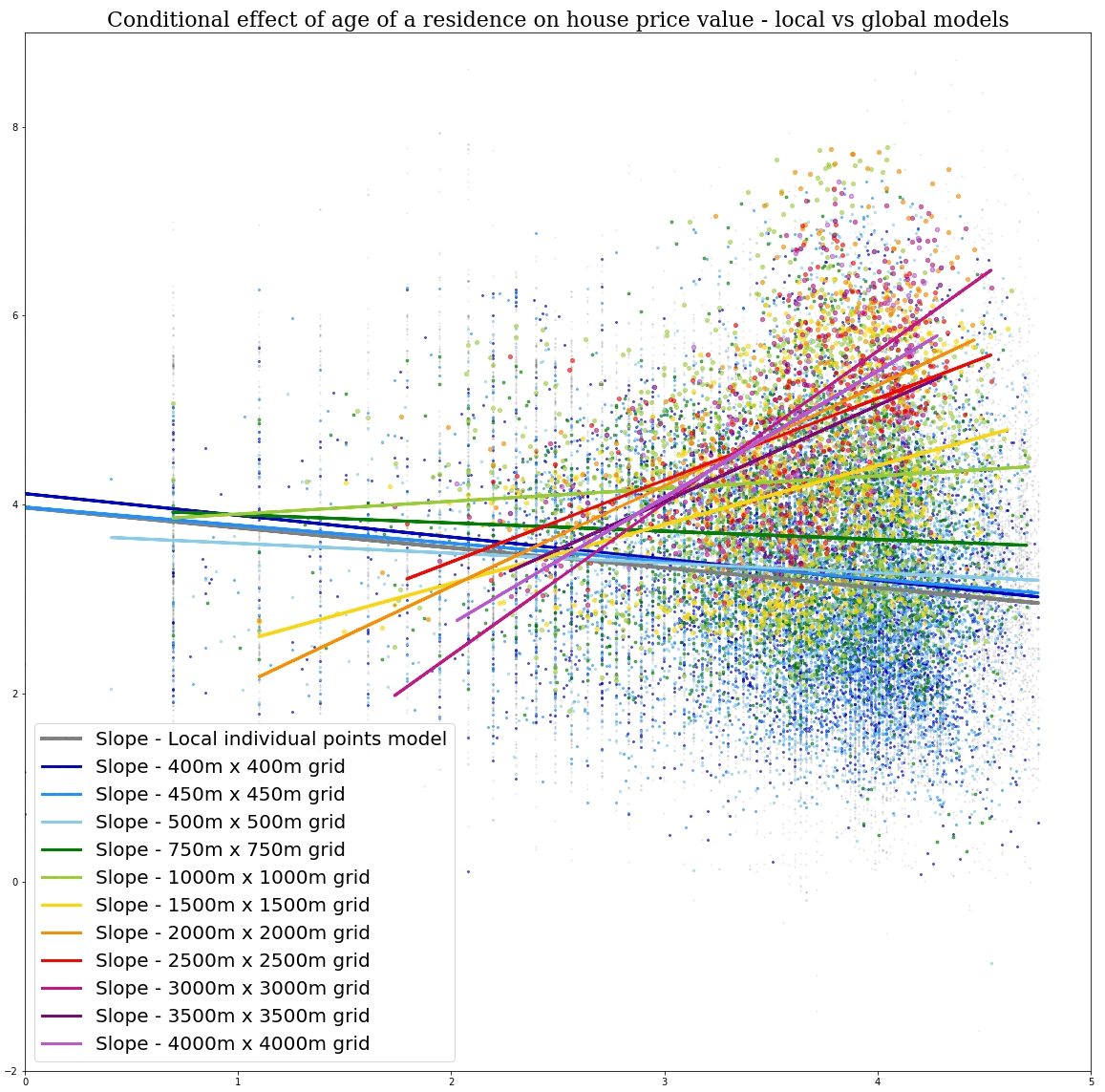
First, we examine the sensitivity of global and local models to the MAUP and show how the effects of the MAUP in global models are a function of the degree to which processes vary over space. This generates a new insight into the MAUP: it results from the properties of processes rather than the properties of data. Then we highlight the extreme differences that can result when calibrating global and local models and how Simpson’s paradox can arise in this context. In the examination of the MAUP, scale is treated as a measure of the degree to which data are aggregated prior to any form of modeling; in the study of Simpson’s paradox, scale refers to the geographical entity for which a model is calibrated.

Please use the link here if the pdf embed does not load: Project presentation