Multiscale Spatially Varying Poisson Model

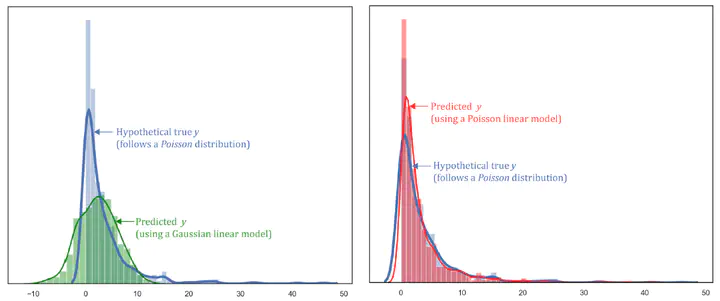
A recent addition to the local statistical modeling framework is the implementation of the Multiscale Geographically Weighted Regression (MGWR) model, a multiscale extension to the widely used approach for modeling process spatial heterogeneity, Geographically Weighted Regression (GWR). MGWR is a local spatial multivariate statistical modeling technique embedded within the regression framework that allows the estimation of parameters at each location using data borrowed from neighboring observations. The extent of neighboring observations used for calibration is interpreted as an indicator of scale for each of the processes being modeled. Using a back-fitting algorithm, MGWR relaxes the restrictive assumption in GWR that all processes being modeled operate at the same spatial scale and allows the estimation of a unique indicator of scale, the bandwidth, for each process. One advantage of the GWR framework, however, is that it can be used to calibrate Gaussian, Poisson and Logistic models, whereas the current MGWR framework is limited to Gaussian models. This research expands the MGWR framework to nonlinear local spatial regression modeling techniques where the response outcomes are discrete (counts following a Poisson distribution). Hence, a major restriction of the MGWR framework is lifted which will provide a richer local statistical modeling framework to model multi-scale process heterogeneity for the open-source spatial modeling community. Use of the new Poisson MGWR model (MGWPR) is shown with a simulated data set and then with Covid-19 case counts within New York City at the zipcode level.

Please use the link here if the pdf embed does not load: Project presentation